orientation angle, which in our case changes to closely follow
the orientation of the Mississippi River. The radar backscatter
is influenced by the local angle of incidence, which will thus
vary as the levee orientation changes with respect to the beam
direction. In order to compute the local incidence angle, we
used the geometric parameters of the satellite orbit combined
with the elevation data from lidar data. The local incidence
angle (
θ
) is the angle between the incident radar beam and the
vertical (normal) to the intercepting surface.
Kriging Interpolation
Kriging is the interpolation method we used to compute
a continuous surface out of the discrete sampling of the
soil conductivity. Such interpolation was needed because
the sample distance for the
EC
measurement points varied,
sometimes being much smaller than the radar resolution cell
and sometimes greater. Kriging is a geostatistical interpola-
tion technique that takes into account both the distance and
the degree of variation between known data points when
an unknown area is estimated. The technique is based on a
weighted linear combination of the identified samples around
the points to be estimated, controlled by a semi-variogram.
By minimizing the error variance, it tries to prevent over or
under estimates (Cressie, 1990).
Back Propagation Neural Network (BPNN)
A back propagation neural network is a multilayer, feed-for-
ward network trained by the error back propagation algorithm
(Fausett, 1993). It is defined by the input, output, and hid-
den layers, and also the weight parameters and the transfer
function. The first layer has weights (W) which are applied to
the input feature values. Depending on the application, dif-
ferent numbers of hidden layers are selected. The weights of
each hidden layer are applied to the outputs of the previous
layer. These parameters are obtained in the training phase,
during which the training data are fed into the input layer
and propagated to the hidden layer and then the output layer
(forward pass). The nodes in the hidden and output layer sum
the inputs from all neurons of their previous layer multiplied
with appropriate weights. The values from the output layer
are compared with the corresponding target values and the
error value between them is back propagated into the hidden
layer (backward pass). This error is used to update the weight
matrices between the layers using the delta rule, which is a
gradient descent method that minimizes the total squared
error of the net output (Fausett, 1993). The
BPNN
used in this
work includes one hidden layer with three neurons, and one
output neuron. Note that we used this simple hidden layer
because some of the
AOIs
have limited reference data samples,
and also for preventing over-fitting. The learning rate was
selected as 0.01. The layer’s weights and biases were initial-
ized according to the Nguyen-Widrow initialization algorithm
(Nguyen, 1990). The tangent sigmoid transfer function was
used for the hidden layer and the linear transfer function was
used for the output layer (Mahrooghy, 2011). The number of
input neurons is equal to the number features used: three for
scenario 1; five for scenario 2; and 35 for the scenario 3 (the
scenarios are detailed in the Results Section). We have 1116,
190, 140, and 311 reference data samples (after interpolation)
for AOI1, AOI2, AOI3, and AOI4, respectively. The training
datasets for each
AOI
comprise 60 percent of the reference
data samples, and 40 percent used for validation and testing
of the
AOI
. The stopping criteria include 100 epochs, the mini-
mum performance gradient of 1 epoch to 6, and maximum
validation failures of 5.
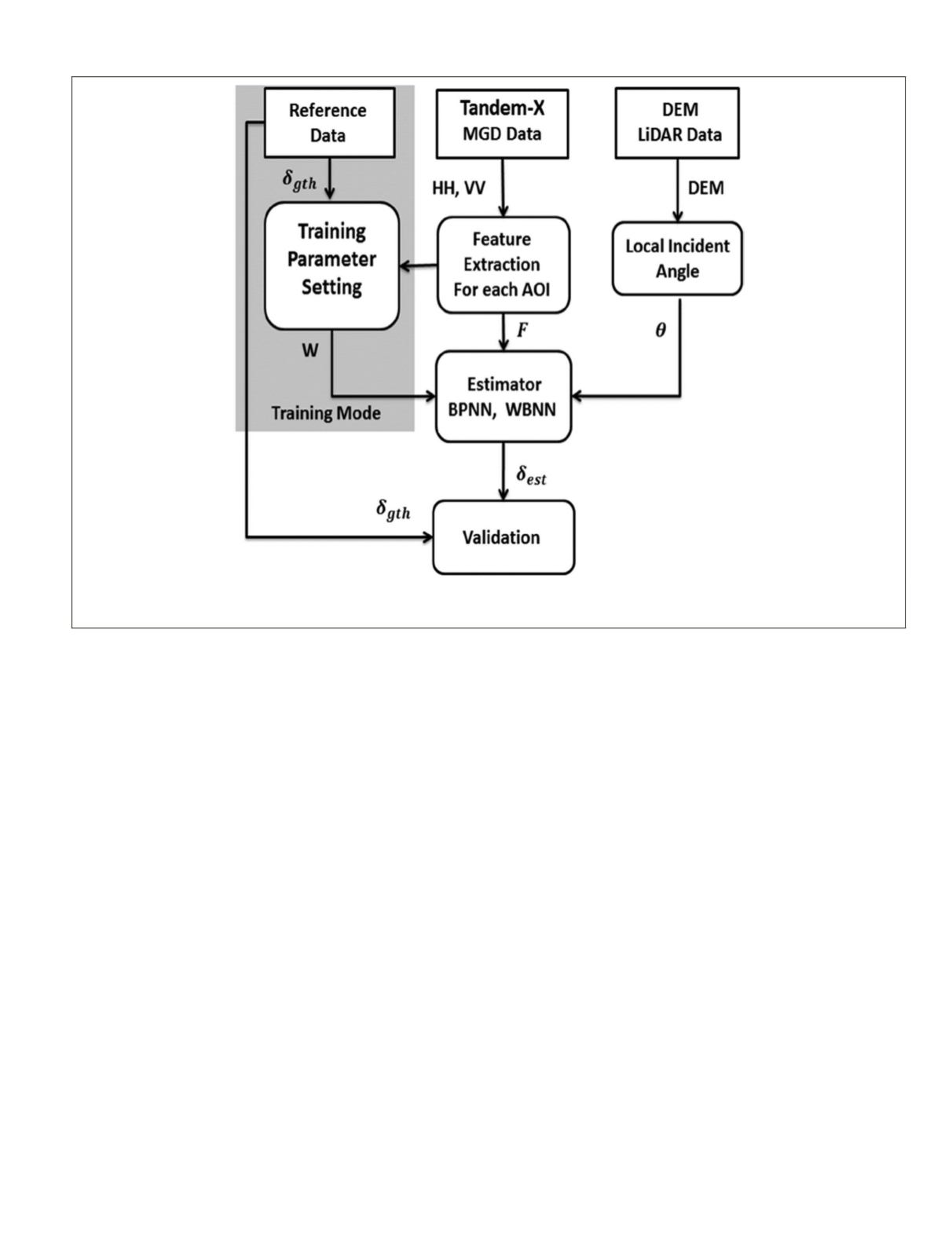
Figure 5. Block diagram of the EC estimation algorithm (
δ
gth
: ground truth soil conductivity; W: Weight for neural network; HH, VV: back
scattering coefficients; DEM: Digital Elevation Map; F: extracted features,
θ
: local incident angle,
δ
est
: estimated soil conductivity; BPNN:
back propagation neural network; WBNN: wavelet basis neural network; MGD: Multi-Look Ground Range Detected).
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
July 2016
513


