658
October 2017
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
SECTOR
INSIGHT:
.
edu
workings of sensors to solidify student understanding of their
capabilities and limitations, and illustrates product fidelity
with respect to a broad range of applications.
Descriptions of error budgets are vital for many geospatial
courses, and should be found at the end of the module for
each given measurement system, ranging from measuring
tape to laser scanners. Likewise, it is important to introduce
undergraduates to basic error theory, least-squares estima-
tion, and the special and general laws of propagation of vari-
ance/covariance. At least one full course should be devoted
to these subjects since they provide the foundation for many
other topics. Sensor models should be described in the under-
graduate photogrammetry courses. Particularly, the funda-
mental photogrammetric frame camera sensor models should
be described: the collinearity equations, which are so common
that it has become customary for authors to refer to them
as the “well-known,” and the coplanarity condition equation.
These, along with laser scanning sensor models, are essential
since graduates are most likely to encounter them in practice,
nowadays. Other, simpler models can also be described such
as 2D and 3D transformations and the direct linear transfor-
mation, but collinearity is emphasized.
In addition to commercial software suites, it is the authors’
experience that in-house software for coordinate transforma-
tion, space resection, relative orientation, space intersection,
and bundle adjustment are extremely beneficial for the stu-
dents. This software can focus more on elucidating what goes
on “behind the scenes” of the photogrammetric processes.
This is extremely useful, since the students and instructor
know exactly what sensor models are being used, and since
detailed reports can be generated highlighting the concepts
described in the lecture and in the readings, including met-
rics not available in the often black-box commercial packages.
Students can then use the known sensor model and accom-
panying measurement uncertainties to predict the propagat-
ed uncertainty in the products, and check against what the
programs report. Similarly, in-house developed visualization
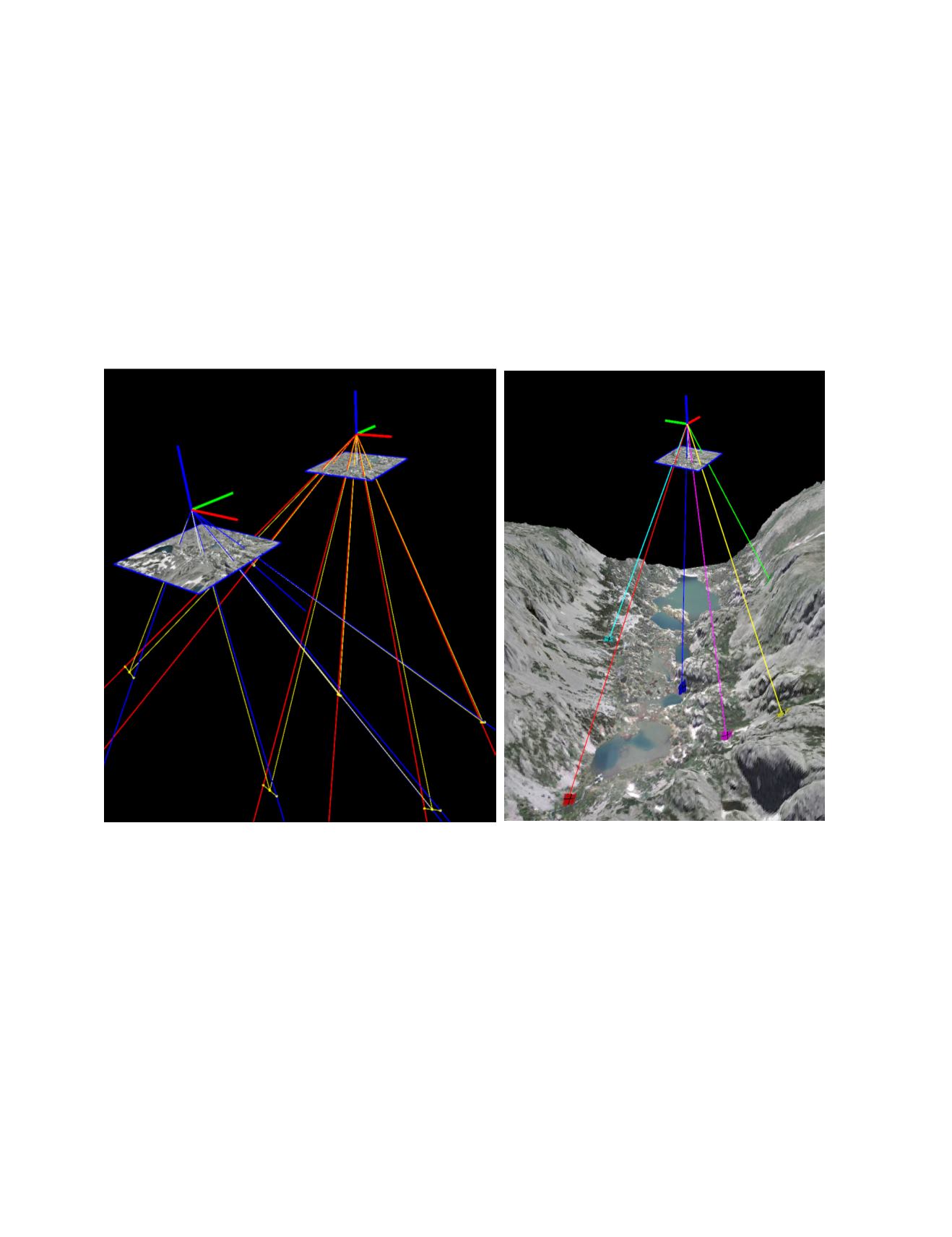
programs with depictions such as those shown in Figure 1,
can be used to illustrate sensor models and error propaga-
tion geometry as an additional resource to strengthen un-
derstanding. So, for example, a student could apply error
propagation equations to estimate the uncertainty in a tri-
angulated point’s position, compare that uncertainty against
what is reported in commercial and in-house software, and
recreate the geometry using the visualization programs for
a graphical representation of the error propagation, thus ac-
quiring an expansive learning experience.
Education in sensor modeling, error propagation, and data
adjustment does not end with Bachelor’s or Master’s degree
geomatics engineering courses, but is also relevant in thesis
Figure 1. Interactive 3D figures, illustrating reprojection error and uncertainty of object space points using the collinearity
model, used in photogrammetry courses at UF to illustrate sensor models and propagation of error. (Computer programs
developed at the University of Florida using data from: Manley, W.F., Parrish, E.G., and Lestak, L.R.,
High-Resolution Orth-
orectified Imagery and Digital Elevation Models for Study of Environmental Change at Niwot Ridge and Green Lakes Valley,
Colorado: Niwot Ridge LTER, INSTAAR, University of Colorado at Boulder, digital media
[
2009
].)


